¡Hola a todos!
Como profesor de matemáticas experimentado, hoy voy a hablaros sobre cómo calcular la tasa de variación media de una función. Antes de empezar, os explicaré qué es para después, poder profundizar en la temática.
¿Buscas clases de matemáticas online?
¿Qué es la tasa de variación media?
La tasa de variación media (T. V. M.) de una función en un intervalo cerrado mide el aumento o disminución de esa función en el mismo intervalo. En otras palabras, estamos viendo qué tan inclinada o "hundida" es la pendiente en un tramo de la función. Medimos qué tanto incrementa la y dividido entre lo que varía la x en una parte específica de la función.
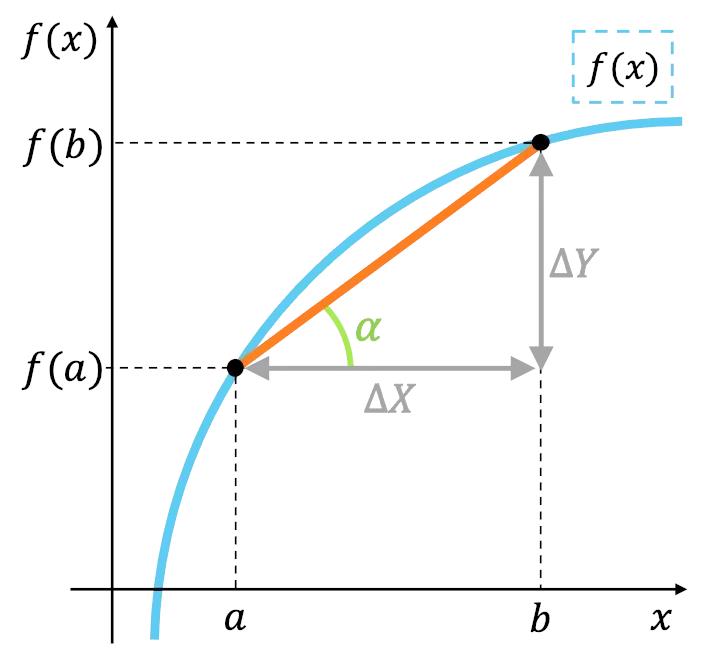
Cómo calcular la T.V.M de una función f(x) en un intervalo [a, b] (versión fácil)
Como ya vimos, la tasa de variación media es lo que incrementa o disminuye la f(x) o "y" respecto a la "x". Es decir, un cociente. Su fórmula es la siguiente:
T.V.M. [a, b] = (f(b) - f(a)) / (b - a)
Truco para memorizar la fórmula: Piensa en la palabra "baba" o "Alibaba". Así sabrás que la b va primero que la a en el numerador y denominador.
Ahora supongamos que se nos pide calcular la T.V.M. de la función f(x)= x^2-x+3 en el intervalo [2, 3]. Se resolvería tal que así:
- Identificar qué es a y qué es b.
- Hallar el valor de f(b).
- Hallar el valor de f(a) (no importa si haces primero el paso 2 y luego el 3).
- Insertar los valores en la fórmula y resolver.
Paso 1: Si nos piden calcularla en un intervalo [a, b], el valor de la izquierda es a y el valor de la derecha es b. Por lo tanto, a equivale a 2, y b equivale a 3.
Paso 2: Hallamos el valor de f(b) insertando el valor de b en la función y resolviendo:
- f(3) = 3^2 - 3 + 3 = 9 - 3 + 3 = 9
Paso 3: Hacemos lo mismo con f(a):
- f(2) = 2^2 - 2 + 3 = 4 - 2 + 3 = 5
Paso 4: Insertamos resultados en nuestra fórmula y operamos:
- (f(b) - f(a)) / (b - a) = (9 - 5) / (3 - 2) = 4 / 1 = 4
La T.V.M. de la función f(x) = x^2 - x + 3 en el intervalo [2, 3] es 4.
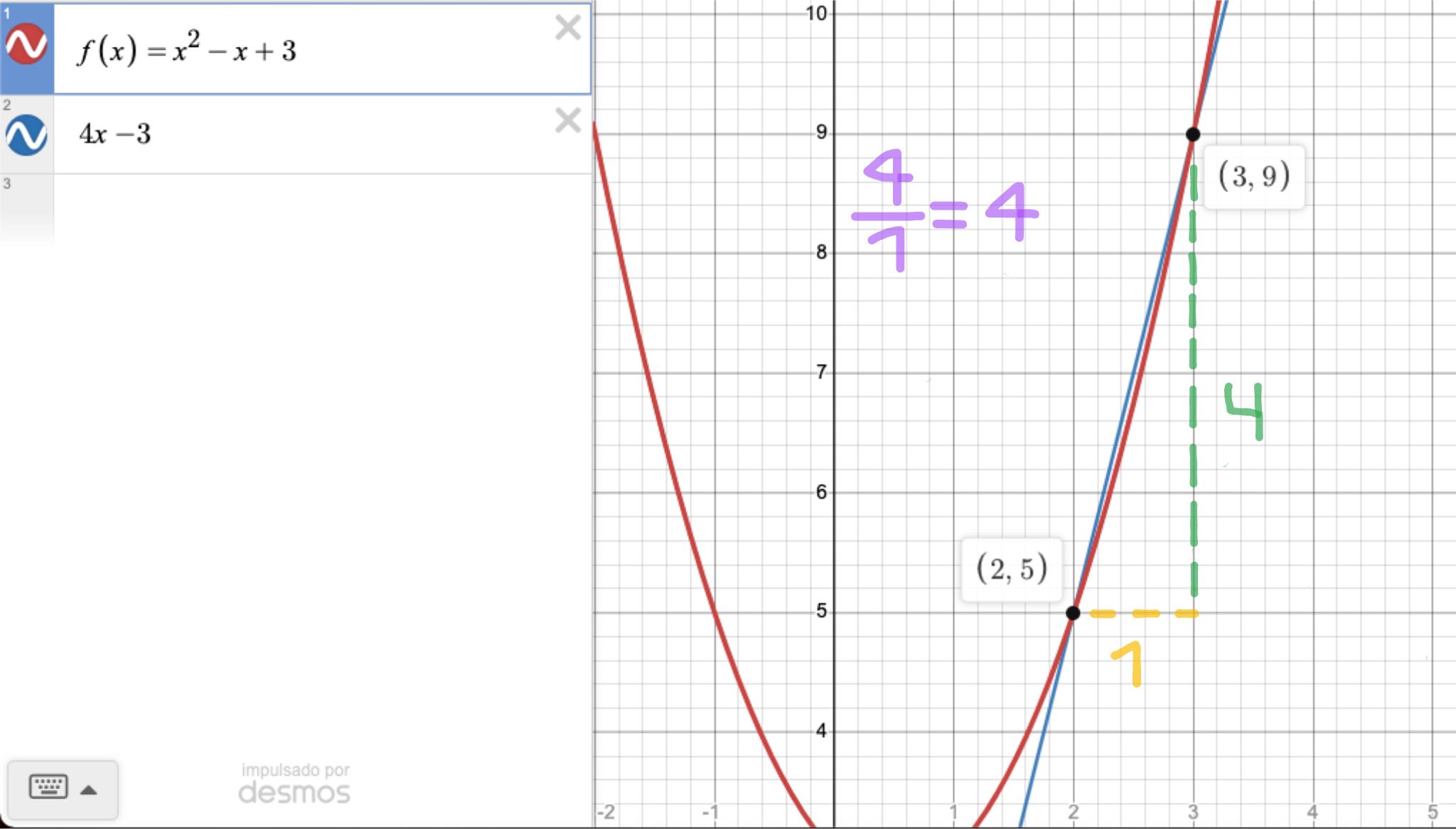
Demostración gráfica
Podemos observar el incremento de la función desde los puntos (2, 5) y (3, 9). La línea roja es la función y la línea azul es la pendiente que pasa por los dos puntos del intervalo (recta tangente), que equivale a la pendiente de la función. Esta recta es la función f(x) = 4x - 3, por lo que tiene un incremento de 4 respecto a la x.
Se ve como por cada unidad que la función avanza en el eje x, la función asciende 4 unidades en el eje y. Es como si por cada gol que marcaras te regalaran cuatro pastelillos.
Nuestra función se desplazó una unidad en horizontal (de 2 a 3) y cuatro unidades en vertical (de 5 a 9). Todo en el intervalo cerrado de [2, 3].
La T.V.M. de una función f(x) en un intervalo [a, a + h] (versión difícil)
Ahora que ya vimos cómo es la T.V.M. con un intervalo cerrado [a, b], veamos cómo se hace con un intervalo [a, a + h].
Hay dos principales diferencias.
La primera es que estamos manejando una incógnita/variable, h, por lo que el resultado de la T.V.M. también contendrá la variable h. Esto puede resultar confuso, pero es así. Como h es variable, el resultado en el que aparece h también lo será.
La segunda implica que tendremos que insertar no solo un número, sino una suma de una letra y un número (a + h) en la operación. Aquí tendremos que ser cuidadosos a la hora de insertar los valores, ya que si lo hacemos muy de prisa o nos despistamos podemos saltarnos signos negativos o potencias. Errores como estos te pueden costar el ejercicio entero en un examen.
Empezar ahora con las clases de matemáticas
Esta vez la fórmula es casi la misma. Solo se cambia f(b) por f(a + h):
T.V.M. ([a, a + h]) = (f(a + h) - f(a)) / (f(a + h) - f(a))
Dicho esto, calculemos la T.V.M. de la función f(x) = x^2 - x + 3 en el intervalo [2, 3]. Los mismos del ejercicio anterior. Seguiremos las mismas instrucciones:
- Diferenciar a de a + h. Esto ya te lo dice el intervalo, por lo que me salto este paso.
- Hallar el valor de f(a).
- Hallar el valor de f(a + h). Por precaución, siempre insertar "a + h" entre paréntesis.
- Sustituir las funciones por los resultados que obtuvimos y operar.
Paso 2: Sustituimos en f(x) el valor de a por el de x y operamos:
- f(2) = 2^2 - 2 + 3 = 4 - 2 + 3 = 5
Paso 3: Sustituimos en f(x) el valor de a + h por el de x y operamos. Poner a + h entre paréntesis:
- f(2 + h) = (2 + h)^2 - (2 + h) + 3 = (4 + 4h + h^2) - 2 - h + 3 = h^2 + 3h + 5
Paso 4: Ponemos nuestros resultados en la fórmula y operamos:
- (f(a + h) - f(a)) / ((a + h) - a)) = (h^2 + 3h + 5) - 5) / (2 + h) - 2 = (h^2 + 3h) / h = (h + 3) / 1 = h + 3
La T.V.M. es h + 3. Este es el resultado final; ya no hay más pasos. El resultado aplica para cualquier valor que tenga h.
Si te resulta confuso, supón que h equivale a 1. Ve a la demostración gráfica de antes y verás que si h equivale a 1. h sería la distancia entre el 2 y el 3. Entonces sería el MISMO ejemplo de antes:
- f(2 + h) = f(3) -> h^2 + 3h + 5 = (1)^2 + 3(1) + 5 = 9
- h + 3 = 4
Cuestiones finales
¿Por qué se le llama intervalo "cerrado"?
Existen dos tipos de intervalos: los abiertos y los cerrados. Los intervalos abiertos incluyen lo que hay dentro de ellos, pero no sus dos puntos extremos. Al contrario, los intervalos cerrados sí incluyen sus dos puntos extremos.
Ejemplo: el intervalo abierto (2,3) incluye a números desde el 2,0000..1 hasta el 2,9999..9. El intervalo cerrado [2, 3] incluye números desde el 2 al 3.
¿Por qué "b - a" y no "a - b"?
Porque medimos la variación entre dos puntos (intervalo) midiendo el valor del segundo punto (o sea, b) con respecto al punto anterior (punto a). Si hacemos la operación haciendo "a-b" nos saldrá la T.V.M. con el signo opuesto.
¡Muchas gracias por leer mi artículo! Espero que te haya gustado y que hayas aprendido algo nuevo. Si quieres que tu hijo o tú empiecen el instituto con apoyo escolar con un profesor particular de matemáticas, no dudes en contactarme a mí o a otro de la plataforma.